How to do Trigonometric Surveying

Trigonometric Surveying: A Step-by-Step Guide
Trigonometric surveying is a method of determining the positions, distances, and elevations of points using trigonometry principles. It is commonly used in civil engineering, land surveying, and construction projects.
Understanding the Basics
Trigonometric surveying relies on angles and distances measured using instruments such as:
- Theodolite or Total Station (for measuring horizontal and vertical angles)
- EDM (Electronic Distance Measurement) devices
- Tape Measures or Chains (for baseline measurements)
- Leveling Instruments (for height determination)
Key Principles & Formulas
a. Distance Calculation Using Angle and Height
If the height of an object and the angle of elevation/depression are known, the horizontal distance can be found using:
Where:
- = horizontal distance
- = height of the instrument
- = angle of elevation/depression
b. Determining Heights Using Trigonometry
For an object of unknown height, using the measured angle of elevation:
Where:
- = height of the object
- = measured horizontal distance
- = angle of elevation
Steps in Trigonometric Surveying
Step 1: Reconnaissance and Planning
- Identify the survey area.
- Choose suitable station points.
- Ensure clear visibility between stations.
Step 2: Establish a Baseline
- Measure a known baseline using a chain or total station.
- Set up instruments at both ends of the baseline.
Step 3: Measure Angles
- Set up a theodolite or total station at one point.
- Take readings of horizontal and vertical angles to target points.
Step 4: Compute Distances and Heights
- Use trigonometric formulas to calculate distances and elevations.
- If required, adjust for curvature and refraction.
Step 5: Plot and Record Data
- Record all readings systematically.
- Plot results on a map or software (AutoCAD, GIS).
Applications of Trigonometric Surveying
- Topographic surveys (mapping terrain features)
- Building height measurement
- Road and bridge alignment
- Boundary surveys
- Hydraulic and dam engineering
Important Considerations
- Instrument calibration: Ensure accuracy of theodolite/total station.
- Atmospheric corrections: Adjust for refraction and earth curvature if needed.
- Error minimization: Use multiple readings and proper leveling techniques.
Conclusion
Trigonometric surveying is a crucial method in civil engineering that enables accurate distance and elevation measurement using angular observations. With modern technology like Total Stations and GPS, its precision has improved significantly, making it an essential technique for land and construction projects.
Definition:
Geodetic or trigonometric surveying considers the curvature of the earth since very extensive areas and very large distances are involved. In geodetic surveying, highly refined instruments and methods are used. Geodetic work is undertaken by the state agency e.g., a survey of Pakistan undertaken by the state agency.
- Triangulation
- Precise leveling
Object:
The object of geodetic surveying is to accurately determine the relative position of a system of widely separated points (stations) on the surface of the earth and also their absolute positions.
Relative positions are determined in terms of azimuths and the length of lines joining them. Absolute positions are determined in terms of latitude and longitudes and elevations above mean sea levels. The methods employed in geodetic surveying are:
- Triangulation (most accurate but expensive)
- Precise traverse (inferior and used when triangulation is physically impossible or very expensive) e.g. Densely wooded country.
Triangulation:
It is based on the trigonometry proposition that one side and three angles be computed by the application of the sine rule. In this method, suitable points called triangulation stations are selected and established throughout the area to be surveyed.
The stations may be connected by a series of triangles or a chain of quadrilaterals as shown.

Baseline:
Whose length is measured these stations form the vertices of a series of mutually connected, triangles the complete figure being called a ‘Triangulation system’. In this system of triangles one line, say ‘AB’, and all the angles are measured with the greatest care, and lengths of all the remaining lines in the system are then computed. For checking both the fieldwork and computation another line, say GH is very accurately measured at the end of the system. The line whose length is measured is known as baseline or base and that measured for checking purposes is known as the check base.
Triangulation Figures:
The geometric figures used in the triangulation system are (i) Triangles (ii) Quadrilaterals (ii) Quadrilaterals, Pentagons, and hexagons with a center angle. This arrangement, although simple and economical is less accurate since the number of conditions involved in its adjustment is small.
- Station adjustment ==> sum of angle is 180
- Figure adjustment ==> sum of angles is 400 grad or 360
- Quadrilateral; adjust ==> (all the angles are horizontal)
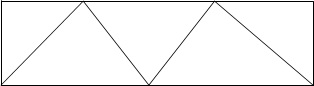 Quadrilateral pentagons or hexagonal with central stations. For very accurate work a chain of quadrilaterals may be used. There is no station at the intersection of diagonals. This system is most accurate since the number of conditions in its adjustments is much greater. To minimize the effect of small errors in measurement of angles the triangles should be well-shaped or well proportioned i.e. they should not have an angle less than 30 or greater than 120. The shape triangle is an equilateral triangle and best shape quadrilateral is square.
Quadrilateral pentagons or hexagonal with central stations. For very accurate work a chain of quadrilaterals may be used. There is no station at the intersection of diagonals. This system is most accurate since the number of conditions in its adjustments is much greater. To minimize the effect of small errors in measurement of angles the triangles should be well-shaped or well proportioned i.e. they should not have an angle less than 30 or greater than 120. The shape triangle is an equilateral triangle and best shape quadrilateral is square.